Please look at Visualization and Graphics Lab page for descriptions of recent research projects. |
|
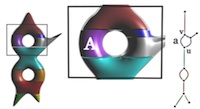   |
Reeb Graphs
Given a smooth real-valued function f over a manifold with or without boundary, the Reeb graph is obtained by contracting the connected components of the level sets to points. It serves as a useful interface to explore large and feature-rich scientific data sets. For 2D domains, we prove tight upper and lower bounds on the number of loops in the Reeb graph that depend only on the surface and describe an efficient algorithm to compute the Reeb graph for piecewise-linear functions. We have also developed generic algorithms to compute the Reeb graph of scalar functions defined over manifold and non-manifold domains. These algorithms are efficient either in terms of worst case running time or exhibit efficiency in practice -- are scalable to large data sets, require a low memor footprint, and are easy implement. We extend the computation to piecewise quadratic functions by constructing a generic tessellation of each element into monotonic patches.
|
 |
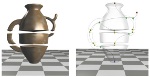
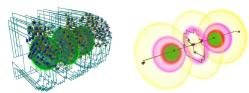
Parallel computation of Morse-Smale Complexes
Data sizes grow faster than processor speeds resulting in an ever-present demand for better algorithms to process the data. With this motivation, we developed parallel algorithms to compute the Morse-Smale complex, a topological structure that has been widely studied and used to represent features in scalar fields. The algorithm utilizes the multiple cores available in the CPU and GPU of a typical desktop computer to compute the MS complex of large two- and three-dimensional data. The definition and computation of the MS complex for sampled functions requires gradient / steepest path computation and path tracing, which is inherently serial in nature. We proved two lemmas on gradient flow paths and symbolic perturbation that lead to an algorithm for computing the cells of the MS complex in a few massively parallel steps.
|
 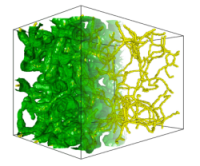 |
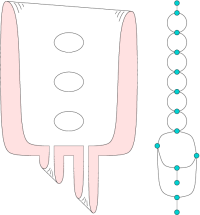
Hierarchical Morse-Smale Complexes
Geometric methods for scalar field simplification do not provide the necessary level of control and hence may result in unnecessary removal of features. We have been working on a topological approach for simplifying continuous functions defined on volumetric domains. The Morse-Smale complex provides an efficient representation of topological features and enables controlled simplification of features. We have developed a combinatorial algorithm for simplifying the Morse-Smale complex that is robust and stable. The simplification procedure leaves important critical points untouched, and is therefore useful for extracting features and storing them in a hierarchy.
|
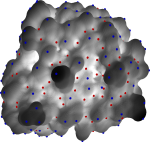 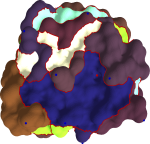 |
Bio-molecular Surface Segmentation
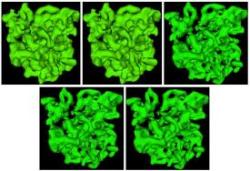
We have developed a new method for segmentation of molecular surfaces. The segmentation is obtained by associating segments with local minima/maxima of an appropriate scalar function defined on the surface. Controlled simplification of the function merges segments resulting in a hierarchical segmentation of the molecular surface. This segmentation is used to identify rigid components of proteins molecules and to study the role of cavities and protrusions in protein-protein interactions.
|
   |
Comparative and Multi-field Visualization
We introduce local and global comparison measures for a collection of k real-valued smooth functions on a common d-dimensional surface. For the special case of k = d = 2 we relate the measures to the Jacobi set, the set of critical points of one function restricted to the level sets of the other. We also extended the topology-based multi-scale analysis methods to this challenging case of multi-field data. We developed a variation density function that profiles the relationship between multiple scalar fields over isosurfaces of a given scalar field. This profile serves as a valuable tool for multi-field data exploration because it provides the user with cues to identify interesting isovalues of scalar fields. We also employed the local comparison measure for robust computation of a multiresolution representation of the Jacobi setcp.
|
 |
Point-based Representations
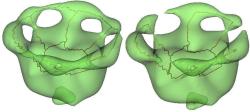
Extracting features from point sets is becoming increasingly important for purposes like model classification, matching, and exploration. We introduce a technique for segmenting a point-sampled surface into distinct features without explicit construction of a mesh or other surface representation. Our approach achieves computational efficiency through a three-phase segmentation process: a topological phase followed by a graph cut and finally a refinement phase. We apply our segmentation algorithm on laser-scanned models to evaluate its ability to capture geometric features in complex data sets.
|
   |
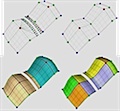
Morse-Smale complexes
Morse functions are used in differential topology to study the topology of manifolds. We use the results from Morse theory to study the topological features of natural phenomena. A Morse-Smale Complex partitions the 3D domain into cells with similar gradient flow characteristics. We design and implement an algorithm for constructing 3-dimensional Morse-Smale complexes with a guarantee on structural correctness. The challenge is to ensure that the discrete approximation of the data does not lead to intersections between the paths.
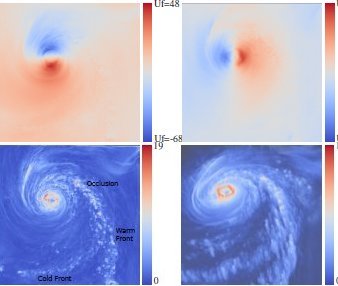
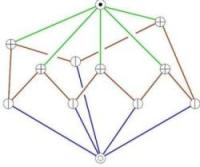
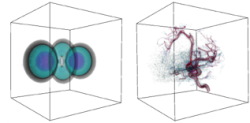
We take advantage of the fact that cells of different dimension in the Morse-Smale complex characterize different types of features present in the data. For example, critical points pinpoint changes in level set topology. Edges of the Morse-Smale complex segment filament-like features that are not explicitly modeled in the original data. Interactive selection and rendering of portions of the Morse-Smale complex introduces fundamental data management challenges due to the unstructured nature of the complex even for structured inputs. We describe a data structure that stores the Morse-Smale complex and allows efficient selective traversal of regions of interest. We illustrate the practical use of this approach by applying it to study cryo-electron microscopy images of protein molecules.
|
 |
Attribute-preserving tetrahedral mesh simplification
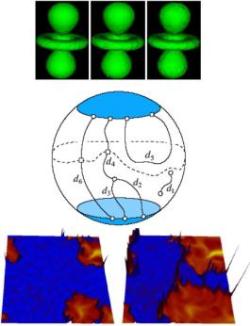
We present an algorithm for the simplification of density maps in 3D. We assume that an input function specified at vertices of a triangulation and linearly interpolated within the tetrahedra. The fundamental operation in the simplification procedure is a topology preserving edge contraction. We describe simple and local conditions that can be used to check if an edge contraction preserves topology. These conditions are derived from the generic link conditions for 3-complexes described by Dey et. al. Besides providing a good approximation of the density map, the algorithm also aims to generate a mesh with good quality elements. We achieve this additional goal using a novel extension of the quadric error metric.
|
 |
Topological analysis of scalar functions for scientific data visualization
Vijay Natarajan. Ph.D. thesis. Department of Computer Science, Duke Univ., Durham, NC, 2004. [PDF one-sided][Hyperlinked] [PDF two-sided][Hyperlinked] [Video 1][Video 2][Video 3] Scientists attempt to understand physical phenomena by studying various quantities measured over the region of interest. A majority of these quantities are scalar (real-valued) functions. These functions are typically studied using traditional visualization techniques like isosurface extraction, volume rendering etc. As the data grows in size and becomes increasingly complex, these techniques are no longer effective. State of the art visualization methods attempt to automatically extract features and annotate a display of the data with a visualization of its features. In this thesis, we study and extract the topological features of the data and use them for visualization. We have three results:
|
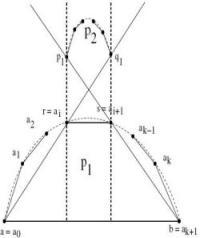 |
Visibility Graphs
We consider the problem of reconstruction of a polygon given it's visibility graph. In general, such a polygon is not unique. We consider a special class of visibility graphs, namely Hamiltonian 2-separator chordal graphs, whose polygons are monotone. We describe parallel algorithms to verify if a given graph is a Hamiltonian 2-separator chordal graph and to reconstruct a polygon from this graph.
|